
Puzzle numerici per il tuo cervello

Puzzle numerici per il tuo cervello
In questa guida offriamo una serie di consigli pratici su come risolvere i puzzle Kakuro, con difficoltà che vanno dal livello principiante a livello esperto.
Per riassumere le regole: Kakuro è un gioco di puzzle su una tavola a forma di cruciverba in cui vengono utilizzate cifre per farle sommare i valori specificati nei quadrati di definizione del tabellone. Inoltre, all'interno di ogni gruppo di somma, ogni cifra può apparire una volta al massimo.
Il modo tradizionale di risolvere un puzzle Kakuro è incrementale: utilizzando le informazioni esistenti sulla tavola, si può trovare con certezza il valore di una cella specifica che può assumere un solo valore possibile. Quindi quel valore viene riempito e il processo viene ripetuto fino a quando tutte le celle della tavola sono state scoperte.
In alcune situazioni, non c'è una cella specifica della tavola con una sola possibilità. In questi casi, ognuna delle possibilità deve essere esplorata da sola ed eliminata attraverso contraddizioni fino a quando non rimane una sola linea d'azione.
Stavano presentando di seguito diversi metodi per fare progressi nella risoluzione del puzzle reale.
Ci sono alcune definizioni che possono essere risolte solo in un modo specifico:
e così via... Di solito puoi passare il mouse su una griglia Kakuro sopra il numero di definizione e apparirà un suggerimento contenente tutte le possibilità di scrivere quella somma con cifre univoche nel numero di celle disponibili.
Le somme che possono essere scritte in modo unico sono di solito piccole somme o somme elevate che costringono cifre basse/alte nella risposta al fine di raggiungerle.
Avere un modo unico di scrivere la somma aiuta, ma tieni presente che tutte le permutazioni sono valide e devi comunque capire quale permutazione effettiva utilizzare sulla lavagna.
 |
 |
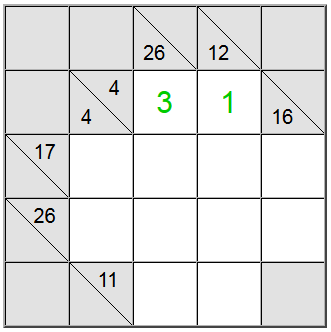 |
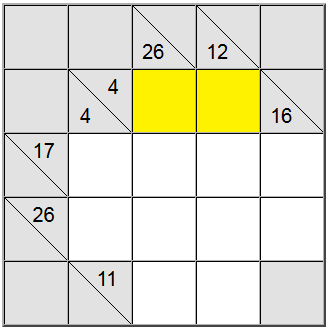
Per le celle gialle evidenziate sopra, c'è solo un modo di scrivere la somma: 4 = 1 + 3. Tuttavia abbiamo ancora bisogno di capire quale permutazione (1 + 3 o 3 + 1) usare.
Risulta che la definizione verticale 26 ci aiuta: una somma su 4 celle che conterrà la cifra 1 sarebbe al massimo 1 + 9 + 8 + 7 = 25. Poiché la nostra somma è 26, si scopre che la cifra 1 non può essere una parte della somma. Pertanto, l'unico ordine rimanente per i quadrati gialli è 3 + 1.
 |
 |
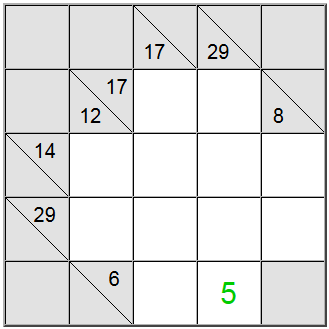 |
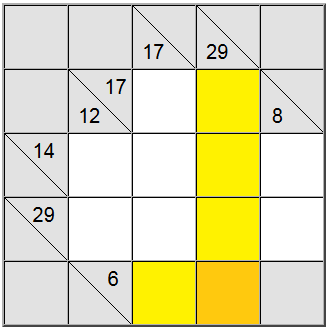
Sulla tavola sopra, i quadrati gialli orizzontali possono essere scritti come 6 = 1 + 5 o 6 = 2 + 4. La somma gialla verticale può essere scritta solo come 29 = 5 + 7 + 8 + 9.
Il quadrato giallo che si trova all'intersezione di queste due definizioni di somma deve contenere la stessa cifra, quindi deve essere presente una cifra comune nelle definizioni orizzontale e verticale per essere condivisa tra di esse. Osservando le possibilità di cui sopra possiamo facilmente capire che 5 è l'unica cifra che rispetta questo criterio.
Questa tecnica funziona particolarmente bene quando si intersecano una bassa somma con una definizione ad alta somma. Le definizioni a somma bassa e alta sono quelle che hanno un numero relativo di definizione a somma bassa o alta (rispettivamente 6 e 29 per il nostro esempio) rispetto al numero di celle disponibili. Poiché 6 è relativamente basso, costringerà cifre basse nella rappresentazione della somma, e 29 forzerà cifre elevate (al fine di raggiungere queste somme usando il numero dato di celle). Pertanto l'intersezione di cifre basse e alte è probabile che contenga solo un candidato per il valore effettivo della cella.
 |
 |
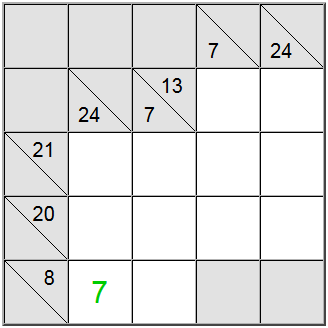 |
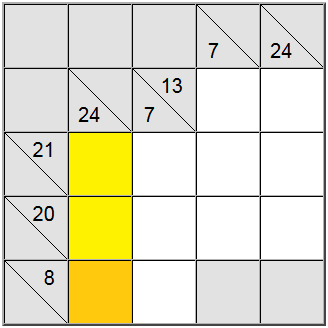
A volte è utile capire il valore massimo o minimo per un gruppo di somma. Questo può darti un senso di ciò che è la gamma valida di cifre per quella particolare somma, che a sua volta ti aiuterà a fare correlazione con altre restrizioni e capire le assegnazioni uniche sulla lavagna.
Nell'esempio precedente, le celle verticali gialle accettano solo valori uguali a 7 o superiori. Se si tenta di assegnare un 6, si può facilmente capire che 6 + 9 + 8 = 23 in modo che la somma di definizione di 24 non sarebbe raggiungibile.
Poiché 7 è un minimo, la definizione orizzontale avente 8 come somma costringe il 7 in quella posizione.
Praticare è il modo migliore per vedere come questo consiglio può essere applicato nei giochi reali di Kakuro. Gioca un puzzle per davvero. Vi auguriamo buona fortuna e tanto divertimento!
© 2026 - Tutti i diritti riservati - Pagina Contatti - Informativa sulla privacy - DE | EN | ES | FR | IT | JA | LT | LV | NL | PL | PT | RO | SV | TR